画像フィルター
フーリエ変換
- フーリエ変換 (Fourier Transform) は
- 信号(画像・データ)を波数(周波数)の異なる成分に分解する
- 実空間 -> 波数空間 (フーリエ変換)
- 波数空間 -> 実空間 (フーリエ逆変換)
フーリエ変換の定義
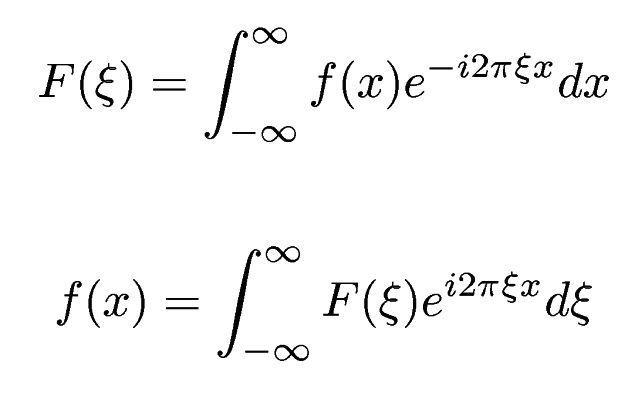
注
- フーリエ変換の定義には
- 波数空間の単位として角周波数(radian)を使うか周期(cycle or Hz)を使うか
- 変換と逆変換で出てくる係数をどのように定めるか
- で、いくつか異なったものがある
- 中身が数学なので、このページの記述をうのみにしないように
フーリエ変換の例(ガウス関数)
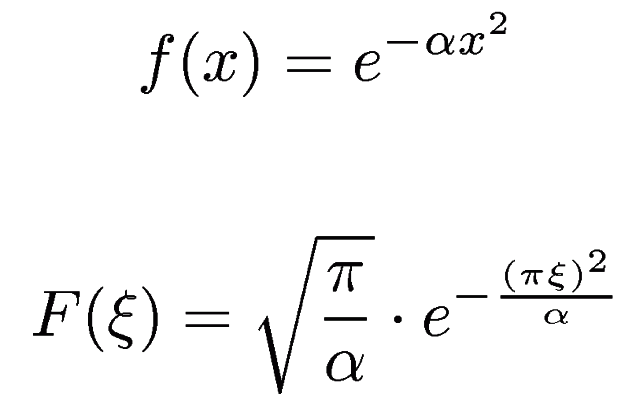
ガウス関数
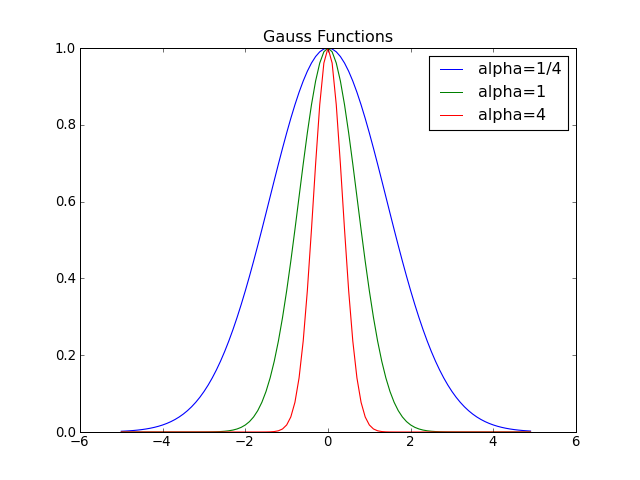
ガウス関数のフーリエ変換
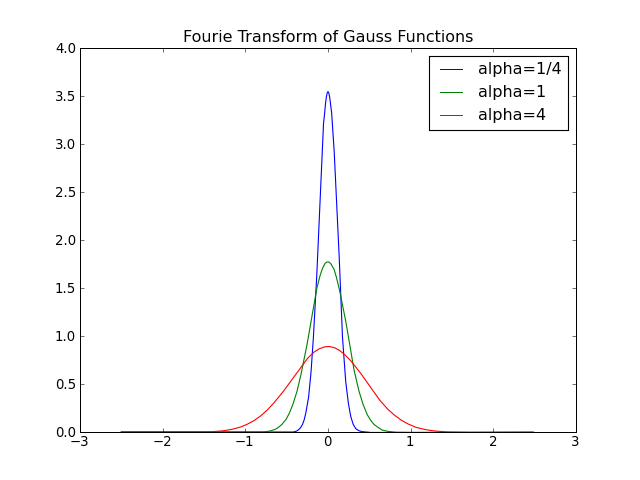
ガウス関数のフーリエ変換の性質
- ガウス(正規分布)関数のフーリエ変換はガウス関数になる
- α(幅を表すパラメータ)の大小で変わる
- 実空間で幅が広い -> 波数空間で幅が狭い
- 大きいもの -> 波数が小さい
フーリエ変換の例(矩形関数)

矩形関数
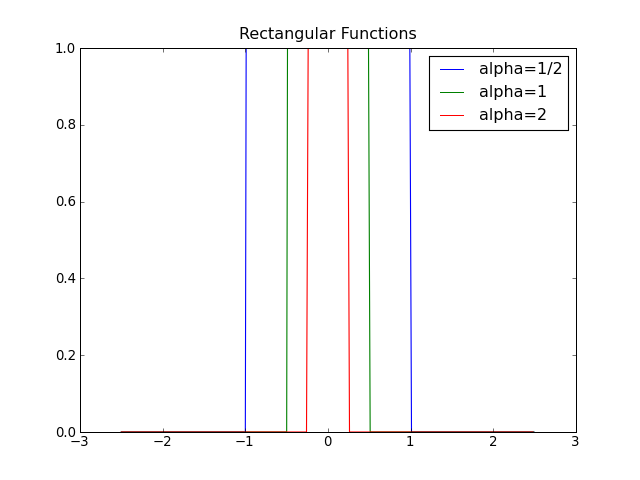
矩形関数のフーリエ変換

フィルター
- フィルター= 「ろ紙」
- 大きいもの(波数小)を通すフィルター (Low-Pass Filter)
- 小さいもの(波数大)を通すフィルター (High-Pass Filter)
- 実際の「ろ紙」では小さいものだけが通る (HPF)
フーリエ変換を使ったフィルター
- G(ξ) = 1 (ξ小), 0 (ξ大) ... LPF
- Fo(ξ) = Fi(ξ) G(ξ)
畳み込み積分

走行平均
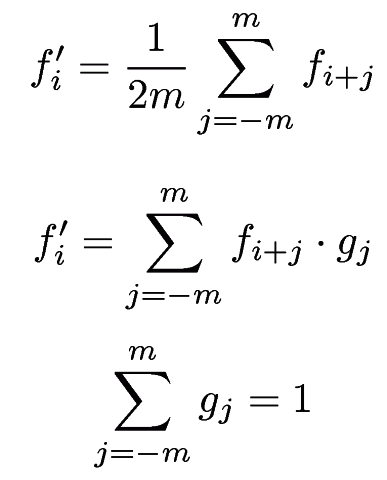
走行平均と畳み込み
- 単純走行平均 ... 矩形関数を用いた畳み込み
- ... フィルター特性 sin x / x
- LPF
- 重み付き走行平均
- 波数空間での特性がよくなるように調整できる
FFT
- Fast Fourier Transform(高速フーリエ変換)
- Discrete Fourier Transform (離散フーリエ変換)の一種(速い)
- FT 無限の実空間 <-> 無限の波数空間
- DFT 空間有限, 標本化有限 <-> 有限波数空間, 離散波数
- (実)空間, 波数空間が無限に繰り返しているとも見える=>フーリエ級数と同じ
FFT の計算例
- 矩形関数
- 1 矩形 (片側)
- 2 矩形 (対称)
- 3 台形 (対称)
- L/2 < x < L の領域は -L/2 < x < 0 の繰り返しと解釈される
FFT を使った LPF
- 原画像

ある断面と、その LPF (FFT)
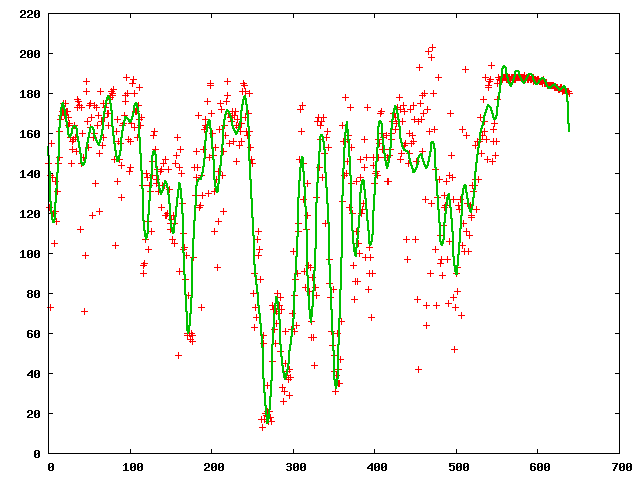
LPF (running mean)
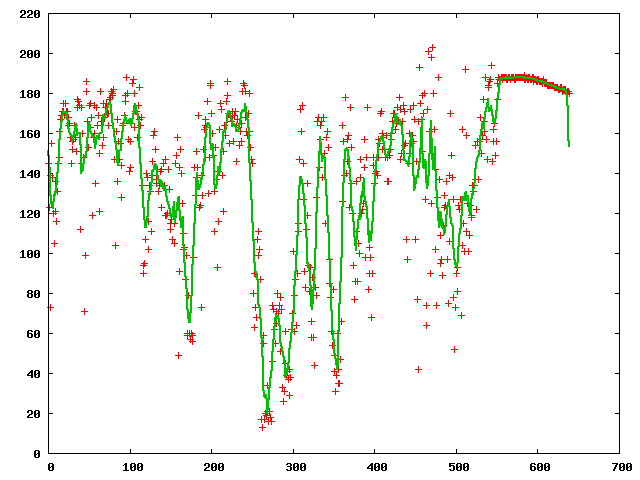
2次元フィルター(原画像)

FFT によるフィルター

走行平均によるフィルター

FFT によるフィルター(改良版)

まとめ
- 矩形関数を用いた FFT フィルターでは波状の「リンギング」が発生する。
- 参考:Gibbs 現象
- 矩形関数を用いるより、なだらかに減衰するような関数を用いたほうがよい。
- ゆるやかなカットオフ (cut off) 特性という
- 走行平均フィルターは高周波成分が残る。
- やはりなだらかに減衰するような関数を用いて畳み込み積分するとよい。
問題
- 用紙は縦長横書き・日付・学生番号・氏名を最初に明記
- 問 次の記述のうち正しいものを選んで書きなさい
- FFT は離散フーリエ変換の高速な計算方法である
- HPF は大きいものを通すフィルターである
- 走行平均は LPF の一種である
- リンギングを抑えるには鋭いカットオフ特性を持つフィルターを使う
解答
- FFT は離散フーリエ変換の高速な計算方法である
- 走行平均は LPF の一種である