画像の幾何補正・他(演習4)
~/image/e4 で演習
内挿法
- Python Imaging Library には内挿法として
- NEAREST ... 最近隣内挿法
- BILINEAR ... 共一次内挿法
- BICUBIC ... 3次畳み込み内挿法
- が用意されている。
- これに加えて、主に画像を縮小するときに使用する ANTIALIAS もある
画像の拡大
- この小さい画像 を 5倍に拡大してみよう
- 最初は NEAREST を使う
# e401.py ... expand image import Image img = Image.open('s401.ppm') width, height = img.size width = width * 5 height = height * 5 imgx = img.resize((width,height), Image.NEAREST) imgx.save('s401-1.ppm')
他の内挿法も試してみる
- 同じ画像を使って、
- BILINEAR -> e401-2.ppm
- BICUBIC -> e401-3.ppm
- ANTIALIAS -> e401-4.ppm
- にそれぞれ画像を保存して比較してみよう
- 注意:img.show() で表示させた場合、いったん JPEG 形式で保存される。このため若干画質が落ちて 比較できないことがある。
画像の縮小と内挿法
- ついでに画像を縮小する場合も比較してみよう
- 大きい画像 をダウンロードして保存し、縦横それぞれ 1/4 に縮小するプログラム(e402.py)を作成しなさい。NEAREST/BILINEAR/BICUBIC/ANTIALIAS それぞれ s402-1.ppm/s402-2.ppm/s402-3.ppm/s402-4.ppm に保存して比較する。
Affine 変換の係数を求める
- 以下の図のような affine 変換を行う
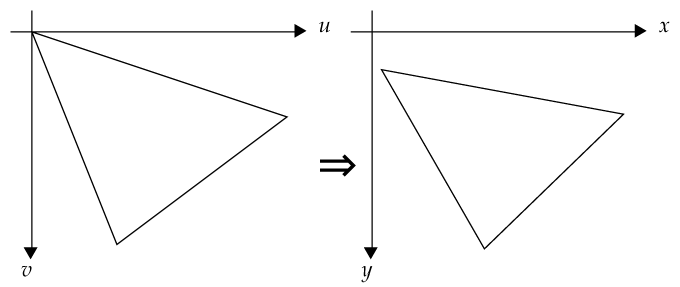
式
u = ax + by + c v = dx + ey + f
- (u, v) -> (x, y) へ変換(逆変換)
三角形の頂点を与える
(x, y) = ( 10, 50), (380, 100), (130, 280) (u, v) = ( 0, 0), (400, 100), (100, 300)
|u1 v1| |x1 y1 1| |a d| |u2 v2| = |x2 y2 1| |b e| |u3 v3| |x3 y3 1| |c f|
- 上記行列による方程式を(a, b, ... f) について解く
Python で解く
# e403.py ... affine coefficients
from scipy import matrix
from scipy.linalg import solve
U = matrix([[ 0, 0],
[400, 100],
[100, 300]])
X = matrix([[10, 50, 1],
[380, 100, 1],
[130, 280, 1]])
C = solve(X, U)
print 'a =', C[0][0]
print 'b =', C[1][0]
print 'c =', C[2][0]
print 'd =', C[0][1]
print 'e =', C[1][1]
print 'f =', C[2][1]
Affine 変換を実行
- PIL の image オブジェクトには transform というメソッドが用意されている。
- 詳しくは マニュアル で
- この画像 を変換
- 係数(a, b,...f) は先に求めたものを使う(このままでは動かない)
# e404.py ... test affine transform import Image img = Image.open('s404.ppm') imgx = img.transform((400,300), Image.AFFINE, (a, b, c, d, e, f), Image.NEAREST) imgx.save('s404-1.ppm')
最小二乗法(おまけ)
最小二乗法(グラフ)
- プログラム例を簡単化し、pylab で点と回帰線を表示する:
# e405.py from math import sqrt from scipy import array import pylab def linreg(X, Y): assert len(X) == len(Y) N = len(X) Sx = Sy = Sxx = Syy = Sxy = 0.0 for x, y in zip(X, Y): Sx = Sx + x Sy = Sy + y Sxx = Sxx + x*x Syy = Syy + y*y Sxy = Sxy + x*y det = Sxx * N - Sx * Sx a = (Sxy * N - Sy * Sx)/det b = (Sxx * Sy - Sx * Sxy)/det return a, b def plot(X, Y, a, b): x = array(X) X0 = x.min() X1 = x.max() Y0 = a * X0 + b Y1 = a * X1 + b pylab.plot(X, Y, 'o', [X0,X1], [Y0,Y1], '-') pylab.show() if __name__=='__main__': #testing X=[1,2,3,4,5] Y=[357.14,153.57,48.78,10.48,-168.8] a, b = linreg(X, Y) plot(X, Y, a, b)