画像再生

画像再生とは（ここでは）

• 画像の元になるデータを集めて
• 画像にする
• SAR （合成開口レーダー）
• CT （コンピュータ断層撮影）
• Fourier Transform

SAR

• Synthetic Aperture Radar
• 合成開口レーダー
• RADAR ... RAdio Detection And Ranging
  • 無線検知測距

普通のレーダー

その表示

• レーダーの表示
• 距離・方位・反射強度

SAR

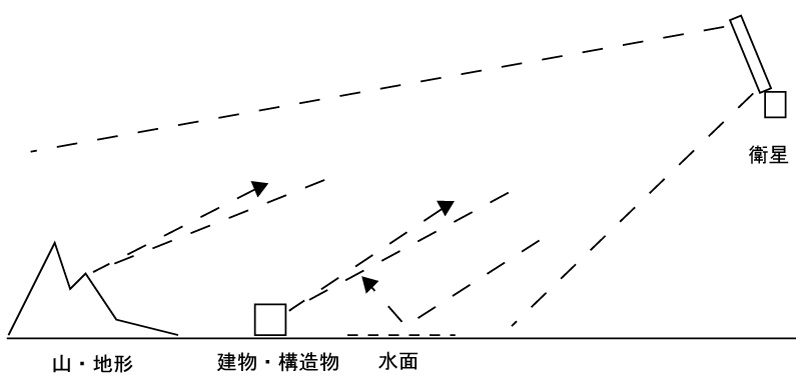
レーダーの解像度

• レーダーの電波は「波」
• D ... レーダのアンテナの幅
• k ... 電波の波数
• dx ... アンテナの一部
• dE ... 電場

レーダーの解像度

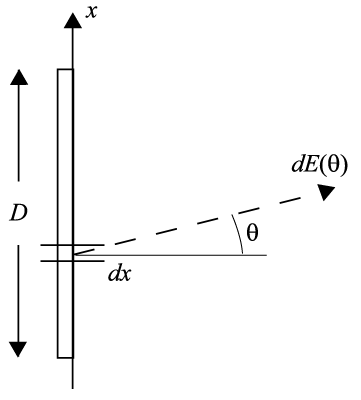
アンテナ幅と解像度

• dE(θ) = a e^{ikx sinθ} dx
  • アンテナの一部から円形に広がる
• E(θ) = ∫ a e^{ikx sinθ} dx
  • -D/2 から D/2 まで積分
• E(θ) = a D sin(kD/2 sin θ) / (kD/2 sin θ)
• 矩形関数のフーリエ変換 ( ../../../kyoko/edu/image/rectt.png ) と同じ

つまり

• アンテナ幅 ... 大
• 電波のビーム幅(θ) ... 小
• 解像度 ... 高い
• 波長 λ = 2π/k
• θ_w = 2λ/D

衛星搭載アンテナ

• D = 10 m, λ=20 cm -> θ_w ～ 0.04
• 高度 800 km とすると 解像度は 30 km 程度

合成開口

• 人工衛星が移動しながら得たエコー（反射信号）
• 大きな D を合成
• D ... 開口(aperture)
• 「合成開口レーダ」
• 合成に必要な反射信号
  • 大きさ
  • 位相

SAR の解像度

• アンテナビーム幅 ... 2λ/D
• 距離(または衛星の高度) ... h
• ターゲットが見える範囲 ... L～2λh/D
• ＝合成されたレーダの開口
• 解像度 ... 2λh/L ～ D
• レーダからの距離によらず、アンテナの大きさ程度
  • Dをいくらでも小さくすればよいというわけではない
  • 小さなアンテナからは利得が得られない

SAR の画像復元

• 基本的には画像の フーリエ変換 が信号として記録される
• なので、逆フーリエ変換することで画像が復元できる
• いろいろあるので、細かいところには触れない

SAR 画像の例

• JAXA ALOS
• NASA SIR-C/X-SAR
  • also - NASA SIR-C/X-SAR
• 干渉SAR

CT

• Computed Tomography
• tomos ... (Greek) 断面
• コンピュータ断層撮影

X線CT

• 物体の影
• I_o = I_i e^-∫f(x,y)dt
• f(x,y) ... 物体のある断面のX線吸収係数分布
• I_i ... 入射 X線
• I_o ... 物体通過後のX線強度

X線CTの測定系

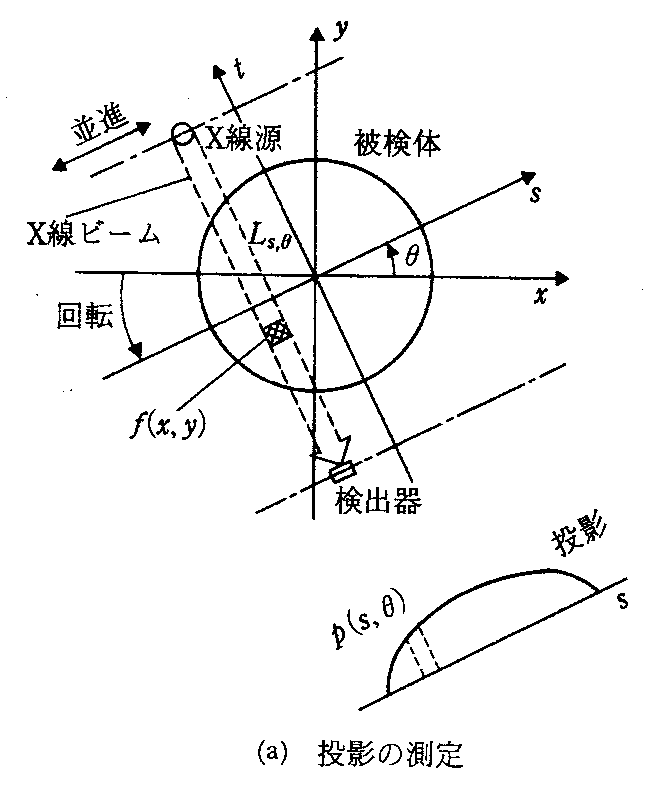
X線源・測定器を回転

• xy座標から角度θだけ回転したst座標を考え
• s軸に投影されたデータ p(s,θ) = -log(I_o/I_i)について考える。
• p(s,θ) = ∫f(s cos θ - t sin θ, s sin θ + t cos θ) dt

フーリエ変換

• p(s,θ)から f(x,y) を求める
• f(x,y)の２次元のフーリエ変換 F(ξ,η)を使う.
• F(ξ,η) = ∬ f(x,y)e^{-i2π(ξx+ηy)}dxdy

波数空間での回転

• p(s,θ) の s に関する一次元フーリエ変換 P(R,θ)
• P(R,θ) = ∫p(s,θ)e^-2πiRsds
• = ∫[∫ f(s cosθ-t sinθ, s sinθ + t cosθ)dt]e^-i2πRsds
• (s, t)->(x, y) 変数変換
• P(R,θ) = ∬ f(x,y)e^{-i2π(xR cosθ + yR sinθ)} dxdy
• = F(R cosθ, R sinθ)

結果

• θ方向の投影データp(s,θ)の s に関するフーリエ変換は
• F(ξ,η)の θ方向での切断面となる
• したがって、θを変えていくことで、F(ξ,η)の全体が求まり、
• その二次元フーリエ逆変換をおこなえば、
• 元の f(x,y)を求めることができる。

結果

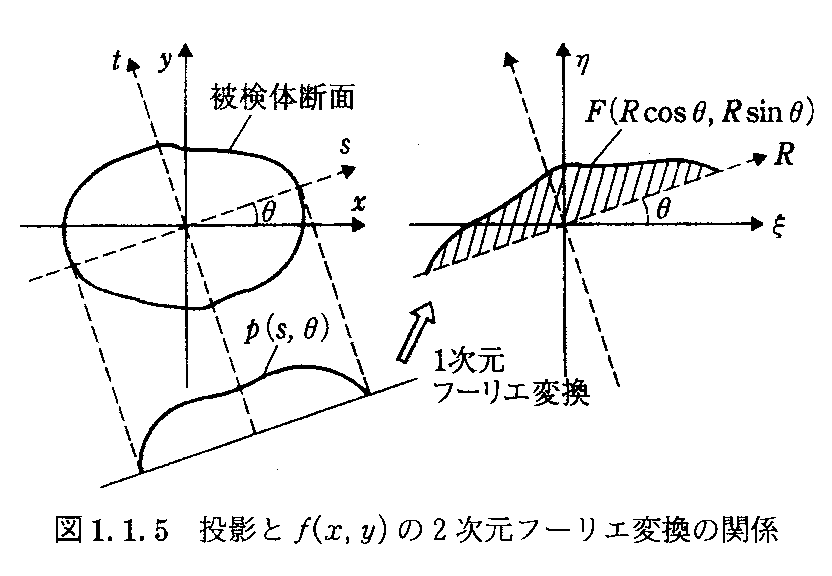
X線CT の方式

最新 CT

• PET-CT
• PET ... Positron Emission Tomography
• こんなのもあった

本日の問題

• SAR や CT の数学的基礎になっているものは
• ______________変換 である。