2
(1) S (n),S (n),・・・, S (n) の中で n で割り切れる個数が 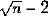 より小さい、
2 4 n-3
より小さい、
2 4 n-3
4 (2) S (n),S (n),・・・, S (n) が全て n で割り切れない、 2n 4n (n-3)n
(3) Vandiver の予想が成り立つ。
n n n 「3以上の自然数 n について、方程式 x + y = z は自然数解を持たない」という 一見簡単そうに見える命題なのですが、 350年にわたって解決を見ていません。 容易に分かるように、 n=4 と全ての奇素数 n について証明されれば良いわけですが、 n=4 のときはフェルマー自身、 n=3 のときはオイラーによって証明され、 コンピュータの発達した今日では、 n ≦ 4,000,000 に対して確かめられています。 今、確かめたと言いましたが、 n をひとつ固定したとしても、 x, y, z の取り得る値は無限にありますから、 有限な計算しかできないコンピューターに乗せるためには 相当な工夫が必要になります。 そのひとつとして、 フェルマーの予想が本質的に難しい問題であることを世に示し、 且つ、飛躍的な貢献を成したクンマーは次の結果を与えました。 結果を述べるために、記号をひとつ導入します2つの自然数 n,k に対して
k k k k S(n)=1 + 2 + 3 +・・・+ (n-1) k
2 奇素数 n について、S (n),S (n),・・・, S (n) が全て n で割り切れないとき、 2 4 n-3 n n n x + y = z は自然数解を持たない。この事実 1 を用いて、実際に調べてみると、 24個ある100以下の奇素数の中で、 37 と 59 と 67 の3個がこの条件を満たさないことが分かります。 しかし、一般には、 この条件を満たさない素数 ( 非正則な素数 ) は 無数にあることが知られていますが、 この条件を満たす素数 ( 正則な素数 ) が 無数にあるかどうかは知られていません。( 注意:S (n),S (n),・・・, S (n) が全て n で割り切れることは 2 4 n-3 比較的容易に証明できます。 )
n n n 非正則な素数 n に対しても、次の3条件を満たすとき、x + y = z は自然数解を持たない。2 (1) S (n),S (n),・・・, S (n) の中で n で割り切れる個数が
より小さい、 2 4 n-3
4 (2) S (n),S (n),・・・, S (n) が全て n で割り切れない、 2n 4n (n-3)n
(3) Vandiver の予想が成り立つ。
現在では、 この事実2 を用いて大きな n までのチェックが出来る訳です。 しかし、事実 1 も事実 2 もその証明には、 代数的整数論の成果に親しまなければなりません。
最後に、上で用いた Sk(n) の変わりに、 ベルヌイ数と呼ばれる数を使うことの方が自然であることを 付け加えておきます。